Hello Toi

Rappel sur la notation
- f(x) : fonction de densité de probabilité
- F(x) : fonction de répartition
Dans le cours, il y a écrit f(x) = 1/(b-a) avec a et b les bornes de l'intervalle de la fonction f. Il s'agit bien de la fonction de densité de probabilté f(x) (et non de la fonction de repartition F(x)).
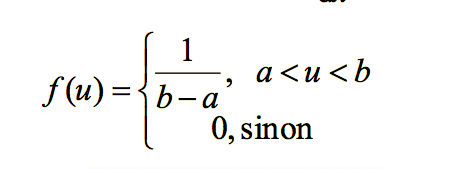
- Capture d’écran 2021-05-17 à 13.10.22.png (14.49 Kio) Consulté 4590 fois
Complément d'information sur la correction du QCS 2:
La loi uniforme continue est loi la plus simple qui existe, tous les événements ont la même probabilité. La densité de probabilité f(x) est donc constante et la fonction de répartition F(x) est représentée par une droite horizontale.
Comme l’intégrale doit être égale à 1 (c'est la condition pour que ce soit une densité de probabilté), la surface du rectangle doit être aussi égale à 1.

Ainsi, la hauteur de f(x) dépend de la largeur de l’intervalle [a ;b].

La largeur étant de b-a, la hauteur doit être de 1/(b-a) pour que le produit soit égale à 1.

La
fonction de répartition, soit l’équation de la droite est égale à
(x-a)/(b-a). En connaissant ça, il n'y a plus besoin de toute la demonstration de la correction.

En effet, il suffit tout simplement de remplacer a par 3 et b par 11 pour trouver la fonction de répartition F(x)= (x-3)/(11-3) = (x-3)/8 .
