Salut :)
Je ne sais pas si tu as remarqué, mais dans toutes les formules de la variance, on divise toujours par
N pour une
variance observée et par
(N-1) pour une
variance estimée. Il en est de même pour la covariance.
On rajoute un -1 dans une estimation pour essayer de limiter les erreurs dues aux fluctuations d’échantillonnage.
/!\ Une variance se note bien sigma^2 (observée) ou s^2 (estimée) alors qu’un écart-type se note sigma ou s.
Cependant la variance et la covariance sont 2 choses bien différentes (malgré leur noms).
La covariance se note cov(X,Y) = sigma(xy) /!\
Tauber a bien détaillé les formules des covariances observées et estimées, cependant il précise bien que sigma(xy) (=la covariance observée)
n’est pas exploitable pour les analyses statistiques, on utilisera donc
toujours s(xy) (=la covariance estimée) et le coefficient de variation
r.
Je te mets les formules de la covariance estimée s(xy) et du coefficient de variation r en pièces jointes, il n’y a que la formule de s(xy) quand le formulaire puisque c’est la seule qu’on va utiliser.
j'espère avoir répondu à ta question !
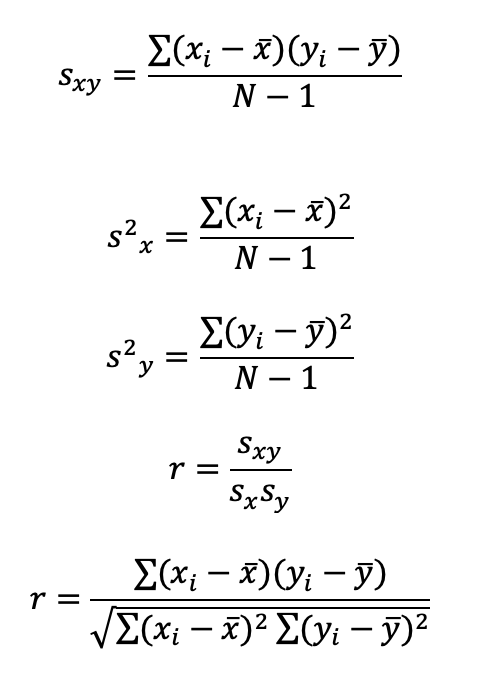
- formules.png (42.67 Kio) Consulté 2592 fois
