Hémodynamique

[rian555]

Saluuut alors j'ai quelques point que je n'arrive pas à comprendre si tu pouvais m'éclaircir ?

- Je ne comprend pas et selon quel formule la raison pour laquelle la viscosité varie avec la température, est ce à cause de la chaleur qu'elle émet ? Mais pourtant il est dit que moins il y a de viscosité et + la température augmente. Et elle peut varier avec quoi d'autres ducoup car il parle de v/x

- La formule du V avec Vmax et la distance entre 2 lames , il pourrait nous demander de la calculer ? Et il nous dit que lorsque la vitesse décroit, la distance entre les 2 lames donc x croit. Hors la vitesse max se trouve ou la distance entre les 2 lames est la plus grande, je ne comprend pas trop. (je suis dans la partie écoulement laminaire, si ca peut t'aider à comprendre ce que je dis)

- Je ne comprend pas la formule de la vitesse critique, elle arrive au moment où la moyenne de la vitesse devient trop élevée est que ca devient turbulent c'est tout ce qui faut comprendre ?

merciiii

[ramoussia]

Saluuuut Rian

Pour ta première question à propos de la viscosité :
D'abord il ne faut pas confondre:
- le lien entre la viscosité d'un fluide et l'émission de chaleur à cause des forces de frottements
et
- l'effet de la température extérieure sur la viscosité d'un liquide.

• Partie du cours sur le théorème de Bernouilli appliqué à un fluide réel

Il est dit que pour un fluide réel donc visqueux tel que le sang, la somme de l'énergie potentielle pgz, l'énergie de pression P, l'énergie cinétique 1/2pv² et l'énergie thermique liée aux forces de frottements, est constante.
pgz + P + 1/2pv² + chaleur = constante
Comparé à la formule pour un fluide parfait, on considère cette énergie thermique car la viscosité du sang entraîne des frottements au niveau de la paroi des artères qui vont dissiper de l'énergie sous forme de chaleur.
Ainsi pour étudier comment les différentes énergies relatives à l'écoulement du sang se compensent, il est important de considérer l'énergie thermique perdue à cause des frottements.

• Partie du cours sur la définition de la viscosité

Ensuite, le professeur Roumy évoque l'influence de la température extérieure sur la viscosité d'un fluide.
Ici, ce qu'il faut retenir c'est que: à l'image de l'eau qui se solidifie lorsque la température diminue (à 0°C, l'eau est solide et ne s'écoule plus, alors qu'à 20°C l'eau est fluide et s'écoule normalement), si un fluide refroidit, le mouvement de ses molécules ralentit et celles-ci se rapprochent les unes des autres et peuvent interagir.
A l'inverse si le fluide se réchauffe, le mouvement des particules accélèrent et les interactions intermoléculaires diminuent ce qui fluidifie le liquide.
C'est pourquoi lorsque la température corporelle augmente, le sang se fluidifie: la viscosité diminue

Enfin la viscosité du sang peut varier également dans un même élément de volume. Par unité de longueur, le volume sanguin peut varier selon la quantité de globules rouges agglomérés:

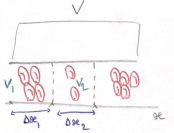
viscosité petit.png (24.99 Kio) Consulté 4759 fois

Ici dans le volume V1, il y a plus de GR agglomérés que dans le volume V2 pour une même distance dx ainsi le rapport dV/dx pour le V1 est supérieur au rapport dV/dx pour le V2 ce qui entraîne des modifications ponctuelles de la viscosité.
--> Donc la viscosité augmente si le rapport dV/dx augmente.

Voilà pour les variations de la viscosité, j'espère que c'est plu clair pour toi

Passons maintenant à ta question sur l'écoulement laminaire
Du fait de sa viscosité, le sang ne s'écoule pas de la même manière entre le centre d'un vaisseau et ses parois .
schématisées dans le cours par deux lames séparées d'une distance x
En effet, les forces de frottements étant maximales au niveau des parois, la vitesse du sang y est minimale.
En revanche plus le sang est éloigné des parois, cad qu'il se trouve au centre du vaisseau à la distance x/2 des 2 parois, moins il est soumis aux frottements avec la paroi donc sa vitesse est maximale .
C'est pourquoi on dit que le front d'écoulement du sang dans un vaisseau est parabolique, plus le sang se rapproche d'une paroi, plus sa vitesse diminue à cause des frottements:

parabole sang.png (13.05 Kio) Consulté 4759 fois

Ainsi pour calculer la vitesse moyenne du sang au niveau d'une section d'un vaisseau on utilise la formule suivante :
V = Vmax x [(1-x)/r²]
Et oui cette formule est à connaître
Elle permet de voir que si un vaisseau est plus grand, la distance x séparant les deux parois augmente, et donc la vitesse moyenne diminue car il y a + de vitesses intermédiaires "petites"(ou du moins inférieures à Vmax) entre Vmax, la vitesse du sang au centre du vaisseau, et Vmin la vitesse du sang au niveau des parois.

j'espère que cette partie est plus claire également pour toi

Enfin pour ta question sur l'écoulement turbulent
Il n'y a pas de formules avec une vitesse critique à savoir, mais en effet pour une vitesse trop importante l'écoulement devient turbulent.
Tu retrouves cette notion avec le nombre de Reynolds qui est proportionnel à la vitesse.

Voilà cette réponse est longue mais j'espère qu'elle t'aura aidé, et si tu as la moindre question n'hésite pas à me relancer!

Bon courage à toi !