Salut Seb !
Je comprends très bien tes questions, on va donc essayer de voir ça ensemble.
Le but de l'exercice est de déterminer λ, la constante radioactive, pour ensuite déterminer la période radioactive T (= demi-vie) que l'on cherche.
- Pour ta première question : "Pourquoi N(t)/N0 = 1/5 ?"

t est une variable, cela signifie qu'il peut prendre n'importe quelle valeur (ici positive), en assurant que l'égalité de départ est toujours vraie.
Ici, l'égalité est la formule N(t)=N0.e^(-λ.t).
Pour déterminer λ, on peut utiliser n'importe quelle valeur de t, mais on va utiliser 1 car l'énoncé nous donne aussi le facteur de décroissance sur 1h, ce facteur est 5.
Cela signifie qu'au bout d'une heure, la population de noyaux est divisée par 5, donc N(t=1) = (1/5).N0 <==> 1/5 = N(t=1)/N0 !
En fait, l'information manquante dans la correction est le choix de t, ici 1.
- Pour ta seconde question : "Pourquoi utiliser ce cheminement de calcul ?"

Comme expliqué au début, le but est de déterminer λ pour en déduire T.
Il faut donc isoler λ dans la formule N(t)=N0.e^(-λ.t) . On obtient alors : e^(-λ.t) = N(t)/N0.
Or, la valeur de e^(-λt) pour t=1 est 1/5 !
On remplace :
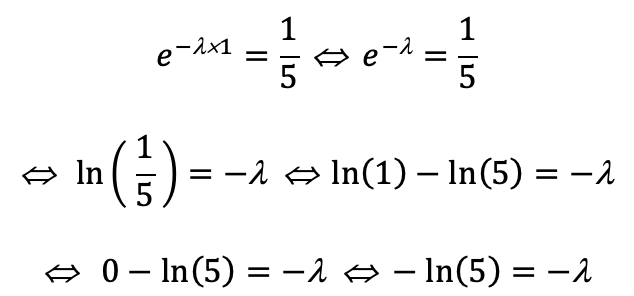
- Calculs.png (21.6 Kio) Consulté 3342 fois
Or, on sait que T = ln(2)/λ = ln(2)/ln(5) = 0,45h !
0,45 x 60 = 27 min
Il est vrai que la correction est assez peu détaillée, mais en appliquant et transformant les formules, on comprend les étapes qui ne sont pas affichées !
- Pour ta dernière question : "t et T représentent la même chose ?"

Je pense en fait y avoir répondu au début

:
- t est une variable de temps, qui correspond au temps passé depuis la mesure de la population N0
- T est une constante, dite période radioactive ou demi-vie, qui correspond à la durée nécessaire pour que la population de noyaux soit divisée par 2.
Voilà, j'espère que mes explications ont été claires, si tu as la moindre question n'hésite surtout pas !
Plein de courage de la part de la Team Biophy !
