Equation différentielle

[Maya]

Salut !
Je me suis rendu compte en faisant des QCM, que je n'avais pas bien compris comment on maniait les équations différentielle.

Merci d'avance !

Screenshot_2020-10-30 Correction Colle 1 Biophysique tHarmo.png (8.63 Kio) Consulté 3002 fois

[Soleil^3]

Coucou Maya !
Je m'excuse pour la latence de ma réponse. Est-il possible que tu joignes à ta question un screen de la correction de ce QCM ? Ainsi nous pourrons reprendre ensemble étape par étape la résolution de cette équation différentielle

[Maya]

Pas de soucis !

Screenshot_2020-11-02 Correction Colle 1 Biophysique tHarmo.png (39.24 Kio) Consulté 2959 fois

[Soleil^3]

Pour trouver la solution générale d'une équation différentielle, il faut procéder par étapes Ces étapes sont listées dans la "Fiche méthode : résolution des équations différentielles" sur laquelle on va s'appuyer pour répondre à ce QCM Notre démarche ne sera donc pas celle exposée dans la correction, cependant le résultat sera le même C'est parti !
Rq : Dans un soucis de nombre de pièces jointes limité, ma réponse se divisera en plusieurs messages, je m'en excuse (je te demande donc de ne pas répondre avant la fin de l'explication )

On part de l'équation proposée dans l'énoncé. On l'appellera (E) pour s'y retrouver. Soit (E) : .



Première étape : Chercher une solution particulière lorsque f(x)=cte

Comme f(x)=cte, f'(x)=0 . On remplace donc f'(x) par 0, ce qui donne . Donc f(x)=0,5 est la solution particulière de (E) lorsque f(x)=cte.



Deuxième étape : Chercher une solution particulière lorsque c=0

Ici, on va remettre notre équation sous la forme f(x)=K.f'(x)+c, avec K et c des constantes, soit .

[Soleil^3]

Suite 2/2

On peut diviser cette deuxième étape en sous-étapes :
1) Mettre sous la forme f'(x)/f(x) afin de faciliter l'intégration
2) Chercher une primitive : on fait apparaître ln(f(x))
3) Remettre sous la forme "f(x)=" : on fait apparaitre la fonction exponentielle

En suivant ces étapes, on obtient alors .


Troisième étape : trouver la solution générale
On y est presque !
Pour avoir la solution de l'équation différentielle il faut faire la somme de la solution particulière lorsque f(x)=cte (solution 1)
et la solution lorsque c = 0 (solution 2). In fine,
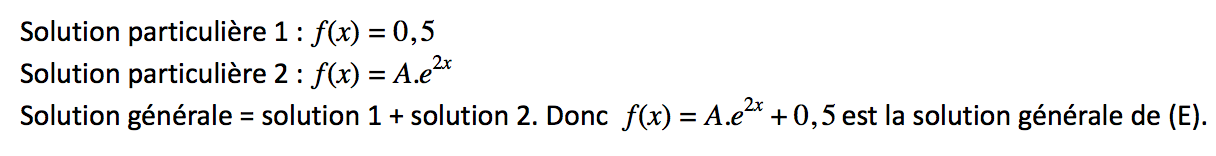
Comme promis, on retrouve le résultat indiqué dans la correction (l'item B est vrai) !

Bonus : Ici, l'énoncé ne fournit pas la valeur de f(0), c'est pourquoi on ne peut pas déterminer la valeur de A.
Si la valeur de f(0) était donnée, il faudrait rajouter une étape dans l'étape trois. Après avoir trouvé la solution générale, on remplace x par 0 afin de trouver la valeur de A. On peut ensuite réécrire la solution générale en remplaçant la constante A par sa valeur


Bravo, tu as tenu jusqu'au bout de cette explication J'espère t'avoir éclairée sur cette notion d'équation différentielle qui n'est pas toujours évidente. Si jamais tu t'es perdue et que tu ne comprends toujours pas, pas de panique ! Fais-le moi savoir et on reprendra ça ensemble
Je tiens à préciser que je te propose ici une des méthodes de résolution, celle qui est selon moi la plus fiable et que l'on vous présente dans la fiche méthodologique

Sur ce ne lâche rien Maya, c'est la dernière ligne droite et ce n'est donc pas le moment de s'arrêter ! Donne tout, la team PC est avec toi et te fait des bisous