Hello Malakestions !
J’espère que tu vas bien, et ta question est très pertinente. On va refaire ensemble un point de cours sur le Chi² d’indépendance.
Lorsque tu as rempli le tableau de contingence, tu dois calculer les
effectifs théoriques. Il y a alors 2 cas de figure :
- si tous les effectifs théoriques sont
supérieurs ou égaux à 5, tu peux calculer la distance du Chi²
sans utiliser la correction de Yates, quelle que soit la dimension du tableau.
- si au moins un effectif théorique est
inférieur à 5, ce que tu vas faire dépend alors des
dimensions du tableau :

dans un tableau
2*2 cases, si tous les effectifs théoriques sont supérieurs à 3, tu peux calculer la distance du Chi² en utilisant la
correction de Yates.

dans un tableau avec
plus de 2*2 cases, tu opères un
regroupement de classes. Pour cela, il faut regrouper les lignes ou/et les colonnes de façon
cohérente, c’est-à-dire qu’il faut toujours que le test effectué réponde à la question de l’étude. Une fois le regroupement effectué, tu recalcules les effectifs théoriques et tu recommences le
même raisonnement : si tous les effectifs théoriques sont supérieurs ou égaux à 5, tu peux calculer la distance du Chi² sans utiliser la correction de Yates ; si au moins un effectif théorique est inférieur à 5, tu peux calculer la distance du Chi² en utilisant la correction de Yates dans un tableau 2*2 cases, ou tu opères un nouveau regroupement de classes dans un tableau de plus de 2*2 cases...
Je te fais un petit résumé du regroupement de classes car ta question portait précisément sur ce point.
Le regroupement de classes s'opère sous 2 conditions :
- Le tableau possède
plus de 2*2 cases
- Au moins un effectif théorique est
inférieur à 5
Ca peut sembler un peu complexe mais tu verras qu’avec la pratique, tu finiras par comprendre le mécanisme. C’est pour ça qu’on va revoir ensemble le QCS 5 de la colle commune. Voici l’énoncé :

- C1.JPG (95.55 Kio) Consulté 3687 fois
Dans cette exemple, on est dans un tableau de 2*3 cases, c’est-à-dire de plus de 2*2 cases. On calcule les effectifs théoriques et on obtient cela :
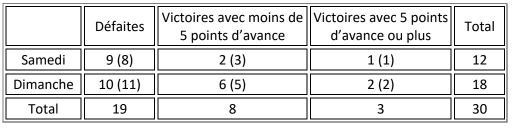
- C2.JPG (25.98 Kio) Consulté 3687 fois
On remarque que plusieurs effectifs sont inférieurs à 5. Comme on est dans un tableau de plus de 2*2 cases, on opère un regroupement de classes. Dans le test, on souhaite évaluer le lien entre le jour du match et son issue. D'après l'énoncé, il y a 3 modalités possibles :
défaites ;
victoires avec moins de 5 points d’avance ;
victoires avec au moins 5 points d’avance. Il est cohérent de regrouper les 2 dernières modalités pour en former une nouvelle qui serait :
victoires. En effet, les modalités
défaites et
victoires caractérise encore bien la variable « Issue du match ». Il n’y a pas de règle particulière à suivre pour le regroupement de classes, mais il faut simplement que le nouveau tableau te semble toujours cohérent par rapport aux variables étudiées.
Je te donne la fin de la correction :

- C3.JPG (120.63 Kio) Consulté 3687 fois
J’espère que je t’ai aidé


La team des Stat’élites te souhaitent bon courage

