Salut Aurélia !! J'espère que tes révisions se passent bien
Ne t'inquiète pas, l'hémodynamique c'est un cours très dense avec pleins de nouvelles notions donc c'est normal si tu comprends pas encore tout mais on va reprendre tout ça ensemble !
1) ☞ Premièrement, la
loi de Bernoulli et la théorème de Bernoulli correspondent bien à la
même chose. Celle-ci nous dit que la somme de l’énergie potentielle
ρ.g.z, de l’énergie de pression
P et de l’énergie cinétique
1/2*ρ*v^2 est constante soit :
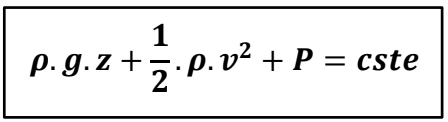
- Capture d’écran 2023-12-01 à 13.04.57.png (12.44 Kio) Consulté 5279 fois
➣ Cette loi implique donc une
conservation de l'énergie. Mais ⚠ attention ⚠, la loi de Bernoulli est définie uniquement pour des fluides parfaits avec un système en équilibre, ce qui n'est pas le cas du sang ! Le sang est un fluide réel et visqueux, auquel on associera une perte d'énergie qu'on nomme
perte de charge, notamment à cause des forces de frottement. On négligera cependant souvent cet aspect pour faciliter les calculs.
☞ Le
phénomène de Venturi permet de
caractériser le sens de l'écoulement. Il découle du théorème de Bernoulli. Il consiste en le fait que l’écoulement d’un fluide se fait des zones de haute pression vers les zones de basse pression mais aussi de la plus grande section du vaisseau vers la plus petite.
L’application du phénomène de Venturi est observée lors de la réduction du calibre d’un vaisseau :
on va avoir une petite réduction de pression qui va
augmenter l’énergie cinétique pour pouvoir respecter la conservation de l'énergie imposée par la
loi de Bernoulli.
☞ La
loi de Pascal quant à elle considère un différentiel de pression
dP entre deux points d’un fluide situés à l’équilibre. Cette différence de pression est générée par la colonne hydrostatique, c’est-à-dire par le poids de la colonne de liquide séparant les deux points. Le Pr. Roumy explique notamment que c'est la raison pour laquelle il y a une différence de pression hydrostatique chez un sujet debout, entre le cerveau et les jambes par exemple. En effet, la colonne de sang appliquée aura une hauteur plus importante au niveau des membres inférieurs qu'au niveau du cerveau. La pression intrinsèque qui en découlera sera donc supérieure vers les membres inférieurs.
➣ En pratique clinique, on utilise la formule suivante qui
découle de la loi de Pascal :
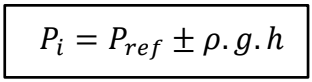
- Capture d’écran 2023-12-01 à 13.24.14.png (9.36 Kio) Consulté 5279 fois
avec
Pi la pression intrinsèque et Pref la pression de référence (celle au niveau du coeur dans notre contexte). On ajoutera donc la pression hydrostatique pour un point situé sous le coeur (ex : les membres inférieurs) et on la soustraira pour un point situé au-dessus (ex : le cerveau).
☞ Enfin, la
Loi de Poiseuille nous dit que la variation de Pression est égale au produit du débit Q et de la Résistance R, soit ∆P = Q*R
Effectivement, elle n'est
valable que dans le cas d'un régime d'écoulement laminaire, qui est le régime physiologique. (L'écoulement turbulent n'est retrouvé qu'en cas de pathologies comme l'anémie, les sténoses ou les souffles ou encore très brièvement lors de la mesure au brassard de la pression artérielle).
2) Concernant la diapo que tu as mise en PJ, elle concerne l'écoulement d'un fluide réel. Le Pr. n'est pas rentré dans le détail de ce qu'est un fluide non newtonien donc pas besoin de trop t'attarder là-dessus. Pour faire simple c'est un fluide qui n'a pas une viscosité homogène mais différente en différents points. On utilise alors la valeur de la viscosité apparente pour les calculs. C'est le cas du sang notamment : il faut se dire que le sang est composé de pleins d'éléments (des protéines, des globules rouges etc) donc il a pas exactement la même viscosité en tout point, on utilise alors une sorte de viscosité moyenne.
Ensuite, le Pr. fait une analogie avec un circuit électrique qui dit que puisque les vaisseaux sont considérés en parallèle et non pas en série, pour obtenir la résistance globale il faudra passer par l'inverse des résistances locales (c'est-à-dire les conductances).
➣
L'inverse de la résistance globale est donc égale à la somme des inverses des résistances locales.
Dans le cadre de cette comparaison, la pression est analogue à la tension électrique et le débit à l'intensité électrique.
*Je te mets l'explication sur le nombre de Reynolds plus bas* 
)
1er point: régulation de la pression artérielle. 
NB dans le cas de ta première proposition, la régulation de la PA correspond à une baisse, donc en réaction on a une vasodilatation pour la faire diminuer. Dans le second cas, c'est ce qui se passe en temps réel consécutivement à une augmentation du débit.