Page 1 sur 1
Régression et corrélation
Publié : 15 avril 2021, 07:37
par Balthazar
Salut les matheux,
J'avais une question par rapport au coefficient de corrélation.
En faisant des QCMS sur tharmo, je me suis rendu compte que des fois quand on avait sigmaX et sigmaY et sigmaXY, on pouvait calculer quand même r, donc on pouvait calculer le coefficient de corrélation estimée, et je n'ai pas compris pq, car pour moi on peut le calculer uniquement si on a les écart-types estimés ??
J'espère m'être expliqué clairement.
Bellleeee journée !!!
Re: Régression et corrélation
Publié : 16 avril 2021, 07:36
par Marionous
Coucouuu,
Il y a deux possibilités de calculer le coefficient de corrélation :

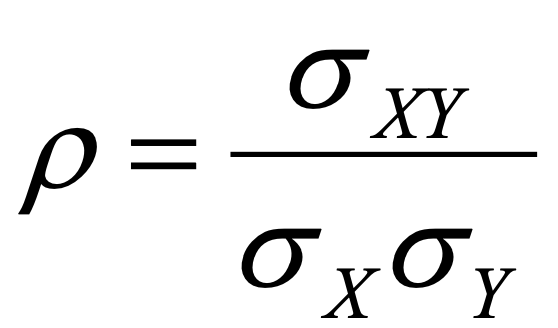
- Capture d’écran 2021-04-16 à 09.21.45.png (19.8 Kio) Consulté 3109 fois
Dans cette formule, on a
𝜎XY qui correspond à la
covariance,
𝜎X à l
'écart-type de X et
𝜎Y à l
'écart-type de Y.
Toutefois, le calcul de la covariance 𝜎
XY est difficilement applicable à l'analyse scientifique, c'est pour cela que l'on va plutôt
estimer la covariance.
On obtient donc une seconde formule :
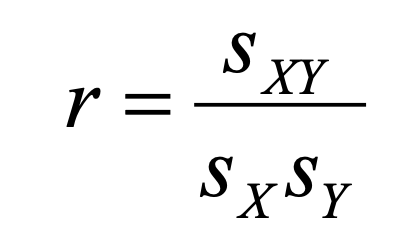
- Capture d’écran 2021-04-16 à 09.25.42.png (12.07 Kio) Consulté 3109 fois
avec :
 sXY : covariance estimée
sXY : covariance estimée
 sX : écart-type estimé de X
sX : écart-type estimé de X
 sY : écart-type estimé de Y
sY : écart-type estimé de Y
Finalement, les deux formules permettent d'obtenir la même chose : le
coefficient de corrélation :
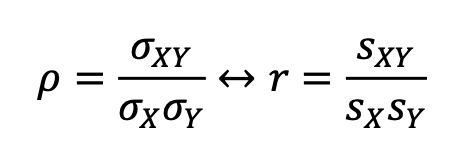
- Capture d’écran 2021-04-16 à 09.31.02.png (10.59 Kio) Consulté 3109 fois
Si dans un exercice, on te donne directement la covariance avec les écart-types correspondant, tu peux utiliser la première formule.
Dans le cas inverse, c'est-à-dire lorsque tu ne connais pas la covariance et que tu dois la calculer, tu dois obligatoirement passer par la seconde formule.
J'espère avoir répondu à ta question

n'hésites pas si tu en as d'autres !
Bon courage pour cette dernière ligne droite, ne lâche rien et on t'envoies plein de force <3333
Re: Régression et corrélation
Publié : 16 avril 2021, 07:47
par Balthazar
Merci pour cette réponse, c'est bcp plus clair !!
J'ai cependant une autre question, le fait d'utiliser r ou p dans la formule pour calculer tc ne change donc rien finalement ?
Re: Régression et corrélation
Publié : 16 avril 2021, 09:10
par Marionous
Non cela ne change rien puisque
r est l'estimation de p.
Dans la majeure partie du temps, il est
très rare de calculer p puisque la covariance ne se prête pas à l'analyse statistique.

Dans le calcul de tc, il faut utiliser le
coefficient de corrélation, et le plus souvent ce sera le coefficient de corrélation estimé r !
J'espère que c'est plus clair

n'hésites pas si tu as d'autres questions !
Bon courage pour cette dernière ligne droite, ne lâche rien et on t'envoies plein de force <3333
Re: Régression et corrélation
Publié : 17 avril 2021, 15:07
par Balthazar
Salutt,
J'ai tout compris, merci de vos réponses, vous êtes les bests <33
Belle journée et bon fin de week-end
