Saluut saluuut Julie !!

Je comprends tout à fait ta question, effectivement ces notations figurent dans le cours sur les lois de probabilités. Ne t'inquiètes pas, on va revoir ça ensemble pour que ces notations n'aient plus de secret pour toi !


Tout d'abord, je te propose de faire un petit rappel de cours sur les lois de probabilités avant de s'intéresser à ces notations :
Les 3 lois de probabilités "classiques" qui ont été abordées dans le cours sont les suivantes :
-La loi
Binomiale : c'est une loi
discrète, entièrement définie par ses
2 paramètres
n et
p, avec n le nombre de fois que l'on répète l'expérience, et p la probabilité de réalisation de l'évènement considéré comme succès de l'expérience
-La loi de
Poisson : c'est une loi
discrète, entièrement définie par son
unique paramètre
m qui correspond à la fréquence de survenue de l'évènement dans un intervalle
-La loi
Normale : c'est une loi
continue, entièrement définie par ses
2 paramètres, l'espèrance μ et l'écart type σ

Une fois ça en tête, on peut s'intéresser à ces notations :
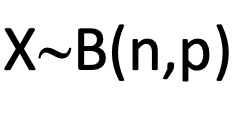
- Capture d’écran 2022-01-18 à 12.21.37.png (10.01 Kio) Consulté 3893 fois
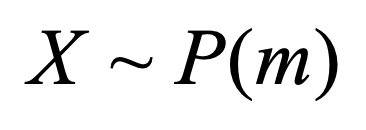
- Capture d’écran 2022-01-18 à 12.21.46.png (12.08 Kio) Consulté 3893 fois
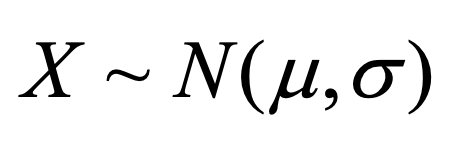
- Capture d’écran 2022-01-18 à 12.21.56.png (14.04 Kio) Consulté 3893 fois
Dans ces notations, il y a plusieurs éléments à identifier, mais le principe reste le même :
-X représente la variable aléatoire
-le symbole "~" se lit et signifie "suit"
-la lettre en majuscule renvoie à la loi de probabilité que suit la variable aléatoire : B pour loi
Binomiale, P pour loi de
Poisson et N pou loi
Normale
-Entre parenthèses sont notés les paramètres qui caractérisent cette loi de probabilité
Si on rassemble le tout, X~B(n;p) se lit : "La variable aléatoire X suit une loi Binomiale de paramètres n et p" !
Voilàa, c'est une notation à savoir lire/traduire si elle est utilisée dans un énoncé. Sinon, tu peux aussi l'utiliser toi même au brouillon par exemple pour traduire rapidement les données d'un énoncé

Petites applications :
- X~B(5;1/3) se lit "la variable aléatoire X suit une loi Binomiale de paramètre n=5 et p=1/3"
- X~P(2) se lit "la variable aléatoire X suit une loi de Poisson de paramètre m=2"
- X~N(10;2) se lit "la variable aléatoire X suit une loi Normale d'espèrance 10 et d'écart type 2"
Voilà voilà, j'espère que ça t'as un peu aidé ! Si tu as d'autres questions, n'hésites surtout pas à nous réécrire sur le forum !
La Team Biostats/Imagerie médicale t'envoie plein de force et te souhaite bon courage !