Coucou Manel !
Ta question est pertinente. On va refaire un point sur les définitions :
La fonction de répartition est la probabilité pour que la variable aléatoire X ait une valeur
inférieure ou égale à un nombre donné x : F(x)=P(X≤x).
Remarque : la probabilité de réalisation d’une variable aléatoire continue X en une valeur particulière est nulle : F(x)=P(X≤x)=P(X<x).
La densité de probabilité est une fonction qui caractérise
une loi de probabilité dans le cas d’une variable aléatoire
continue. Ainsi, elle est régie par les axiomes de Kolmogorov.
Remarque : on note généralement la fonction densité de probabilité : f(x).
De plus, il y a une équivalence entre
une somme dans le cas
discret et
une intégrale dans le cas
continu. Ainsi, pour une variable aléatoire X continue :
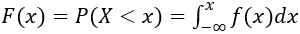
- VA 1.JPG (10.8 Kio) Consulté 1984 fois
Il en découle que :
La fonction de répartition est égale à
l’intégrale de la fonction densité de probabilité.
La fonction densité de probabilité est
la dérivée de la fonction de répartition.
Remarque : sur un graphique, la fonction densité de probabilité correspond à la
courbe, et la fonction de répartition correspond à
l’aire sous la courbe.
Voilà, j’espère t’avoir aidé à bien comprendre ce point du cours
Les Stat’élites de Staturne te donnent plein de courage pour la fin du semestre
