Salut Simon !

J’espère que tu vas bien et que tes révisions se passent bien !!

On va essayer de revoir ce QCS ensemble pas à pas :

Tout d’abord ici on utilise la
loi binomiale qui est définie par
2 paramètres :
n qui correspond au nombre de tentative et
p qui correspond à la probabilité de succès et dont la formule est :
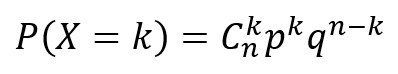
- Capture d'écran 2024-01-31 182729.png (4.22 Kio) Consulté 6853 fois

Ce à quoi il faut bien faire attention avec la loi binomiale c’est de bien
lire l’énoncé pour bien associer quelle valeur correspond à quoi. Ici, on dit qu’on cherche la probabilité qu’elle ne prenne PAS de kiwi, le
succès correspond donc au fait qu’elle ne prenne pas de kiwi et
l’échec correspond au fait qu’elle prenne un kiwi ce qui veut dire que p = la probabilité qu’elle ne prenne pas de kiwi et
q = 1-p = la probabilité qu’elle prenne un kiwi. La variable k correspond quant à elle au nombre de succès.

Si on
traduit littéralement l’item : P(X=4) signifie en fait la probabilité qu’elle ne prenne pas de kiwi pendant 4 jours parmi les 14 jours. En biostatistiques c’est parfois difficile de se rendre compte de ce qu’on nous demande quand on ne voit que des formules devant nous donc n’hésites pas à traduire littéralement ce que tu vois pour mieux comprendre


Pour résoudre l’item il nous faut donc faire l’
application numérique de la formule que j’ai citée au-dessus. Pour cela il faut qu’on sache les valeurs numériques de k ; p ; q et n. La valeur de n est donnée dans l’énoncé avec la phrase « lorsqu’il compte sur 14 jours » donc n=14 et la valeur de k est donnée dans l’item : k=4. Il nous manque donc les valeurs de p et q. Cependant, une des caractéristiques de la loi binomiale est
E(X)=np or l’espérance nous est donnée dans l’énoncé donc on peut déterminer la valeur de p puis trouver celle de q car q=1-p comme expliqué dans la correction. Une fois qu’on a bien toutes nos valeurs numériques on peut passer à l’application numérique comme détaillé dans la correction en faisant bien attention à ne pas confondre les probabilité de succès et d’échec, c’est un piège très fréquent !

J'espère que ma réponse t'aidera ! Si ce n'est pas clair ou si tu as d'autres questions n'hésites pas à revenir vers nous
 La team Biostat' te souhaite bon courage !! <3
La team Biostat' te souhaite bon courage !! <3