Salut!! On va reprendre tout ça ensemble

Ce QCS concerne le
test non paramétrique de Spearman que vous n'avez pas encore abordé en cours donc c'est normal si tu n'as pas tout compris. Je vais néanmoins t'expliquer tout ça pour qu'il ne te pose pas problème quand vous l'aurez vu !

Dans ce QCS, on réalise donc un test de Spearman, il est utilisé lorsqu’il n’y a pas de normalité de distribution qui est une condition de la réalisation du
test de Pearson; ce dernier est donc ici irréalisable.
Le test de Spearman est la version non paramétrique du test de Pearson.
On utilise pour ce test la formule suivante :
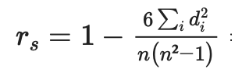
- Capture d’écran 2024-02-13 à 11.01.20.png (9.65 Kio) Consulté 2060 fois
Cette formule nécessite de connaître la
taille de l’échantillon (=n) et les
différences individuelles entre les rangs (=di) de chaque valeur, c'est-à-dire la différence entre les rangs des différentes variables pour un même individu. Pour ce faire, il va ainsi falloir assigner des rangs aux différentes valeurs des variables.
Ici, les variable à classer sont l'âge et la durée de la tournée. On donne donc un rang à l'âge allant du plus petit au plus grand. Le plus petit âge est 26 donc il prend le rang (1) puis 32 prend le rang (2) et ainsi de suite. Puis on range les durées de tournée suivant la même logique, du plus court au plus long.

Dans le cas où différents individus ont la même valeur pour une même variable (comme ici Fred et Hector ont tous les deux une durée de tournée de 6h30) il va falloir leur assigner le rang moyen (le rang réel + le rang supérieur le tout divisé par 2) ce qui fait un rang de (3+4)/2=3,5 pour Fred et Hector.
Il ne reste plus qu'à appliquer la formule (

qui se trouve d'ailleurs
dans le formulaire que vous aurez à l'examen)
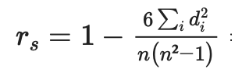
- Capture d’écran 2024-02-13 à 11.01.20.png (9.65 Kio) Consulté 2060 fois
Pour calculer
di on fait donc la différence entre les rangs propres à chaque personne; par exemple pour Fred on fait 2-3,5 = -1,5; comme
di est finalement mis au carré on peut se débarrasser du
- ce qui fait 1,5^2. Et on suit la même logique pour chaque individu. On fera ensuite la somme de toutes les différences de rang et il ne faudra pas oublier de multiplier le tout par 6 ! On soustraira enfin le résultat obtenu à 1.
Voilà j'espère que c'est plus clair pour toi, si non ne t'en fais pas attends de voir le cours et relance moi si tu as encore des questionnements dessus

Je t'envoie beaucoup de force !!

Diana